Three Geysers (Solution)

\[\begin{align*} A &= 23/36 \\ B &= 8/36 \\ C &= 5/36 \\ \end{align*}\]

You can read Presh Talwalkar’s solution here.

My solution

First things first, geysers every 2, 4, and 6 hours is no different than 1, 2, and 3, and those are easier to work with, so for my solution I’m assuming A, B and C erupt every 1, 2, and 3 hours respectively.

Just 2 geysers

To start, let’s simplify the problem and consider the case with just two geysers A and B which erupt every 1 and 2 hours respectively.

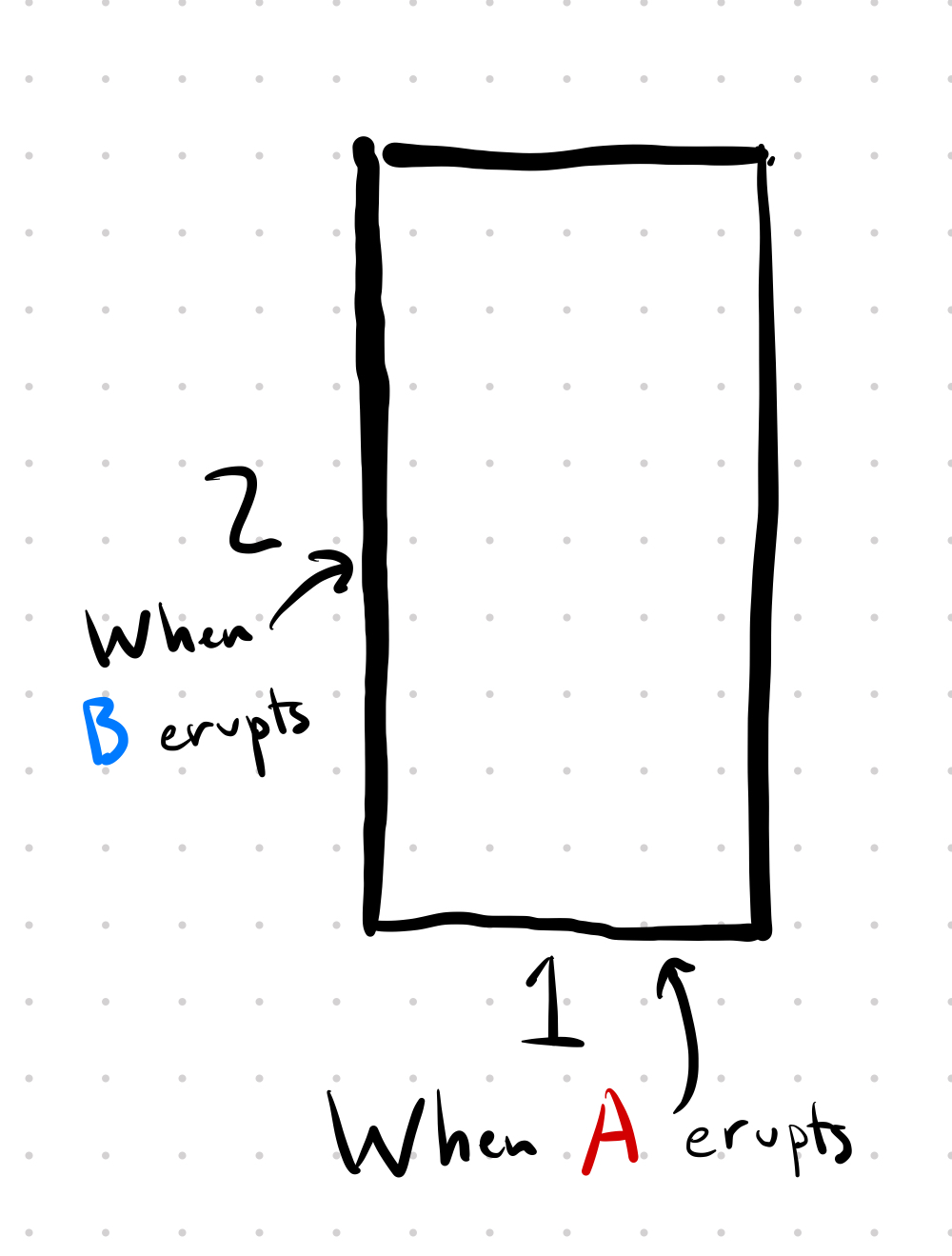
We arrive at the park and have no idea when each geyser will erupt, but we know that geyser A will erupt sometime between now and 1 hour from now, uniformly distributed over that time interval, and geyser B will erupt sometime between now and 2 hours from now, also uniformly distributed over that time interval. Furthermore, the question said the geysers erupt independently.

We can visualize this as a 1x2 rectangle where the x-axis represents when A will erupt next and the y-axis represents when B will erupt next. Like so:

Just to make sure you understand what this represents, consider the point (0.8, 1.6):

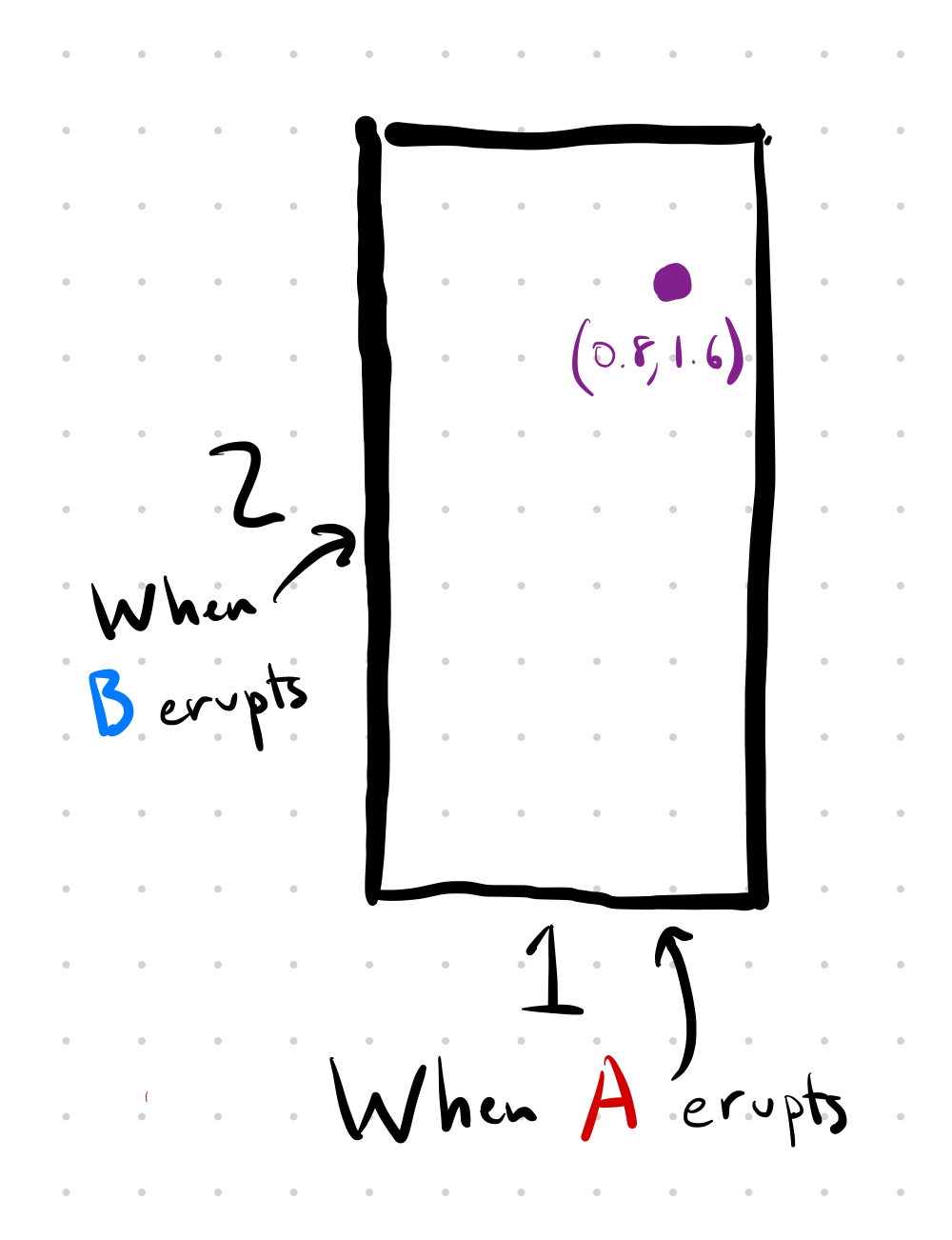
That point represents the outcome where A erupts after 0.8 hours and B erupts after 1.6 hours.

We can shade the rectangle according to which geyser will erupt first. The red region is when A < B and therefore A erupts first. The blue region is when B < A and therefore B erupts first. Notice that the dividing line between the two regions is when y = x.

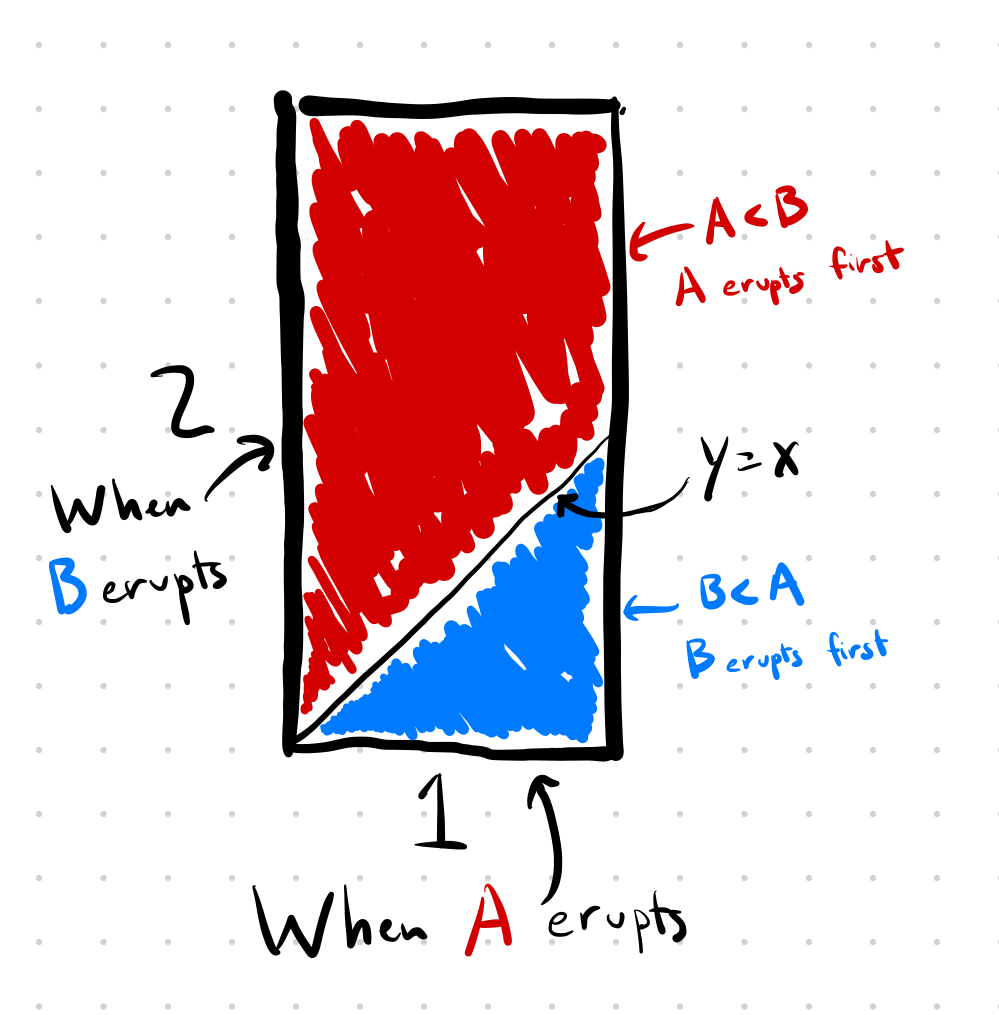
To compute the probability B arrives first, all we need to do is compute the area of the blue region and divide by the total area of the rectangle: \(\frac{1/2}{2} = \frac{1}{4}\). Likewise for the probability that A arrives first: \(\frac{3/2}{2} = \frac{3}{4}\).

Now with 3 geysers

We can solve the real problem (with all 3 geysers A, B, and C) in exactly the same way. It’s just much harder to visualize since it’s in 3D.

Instead of a 1x2 rectangle, we need a 1x2x3 box. I’d attempted to draw the shape from two different angles. Like in the 2D case, I colored each point as red if A erupts first, blue is B erupts first, and green if C erupts first:

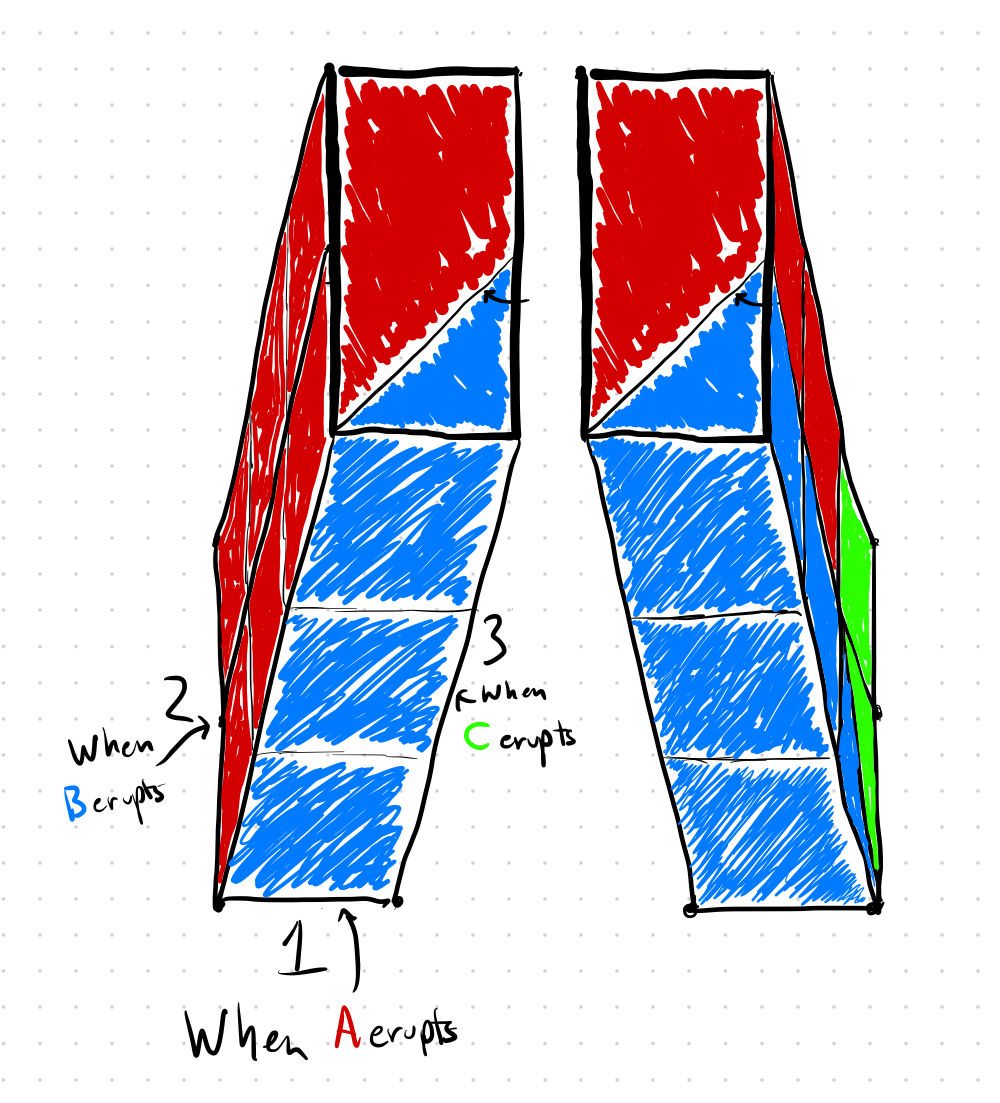
I’m not good at drawing, but also it’s kind of hard to get a sense of how the inside of the box is colored just by looking at the outside, here’s a video of the same shape but I’ve shunk each 1x1x1 cube so that you can effectively look inside the box:

(credit for the awesome visualization goes to Ian Henry who helped me make this using his very own https://bauble.studio/)